Let's Draw a Rose
Here comes the magic. Our first sketch is inspired by this John Whitney creation:
To start, we will draw a circle. Usually in creative code we begin by drawing an ellipse, but today we will draw a circle with a trigonometric equation.
Since the circle will be drawn from a series of points, we need to use a for loop. If you're unfamiliar with for loops, learn more here.
We need to calculate every point of the unit circle and sketch each of them individually. To find those points, we will use these equations:
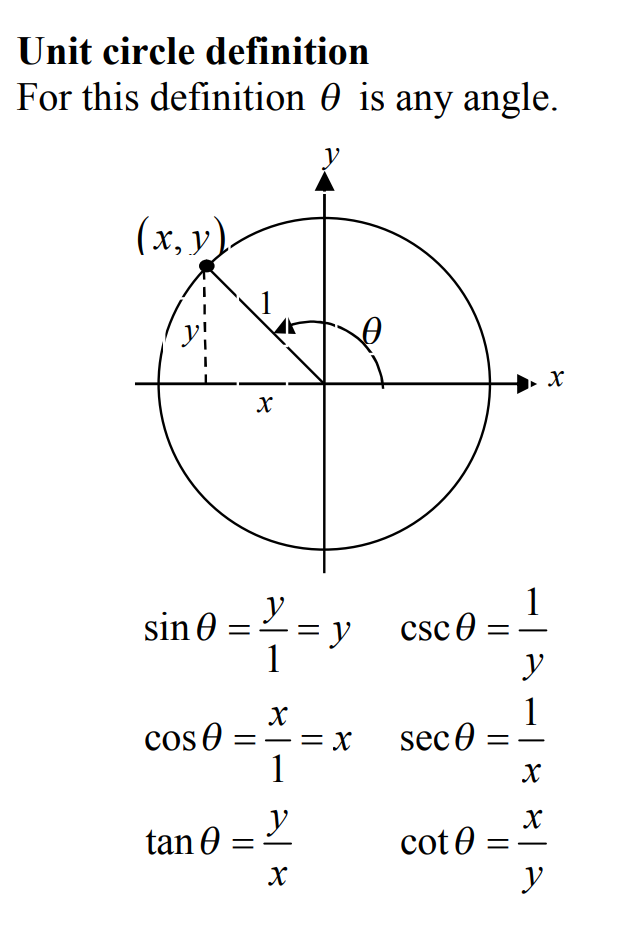
Image Source
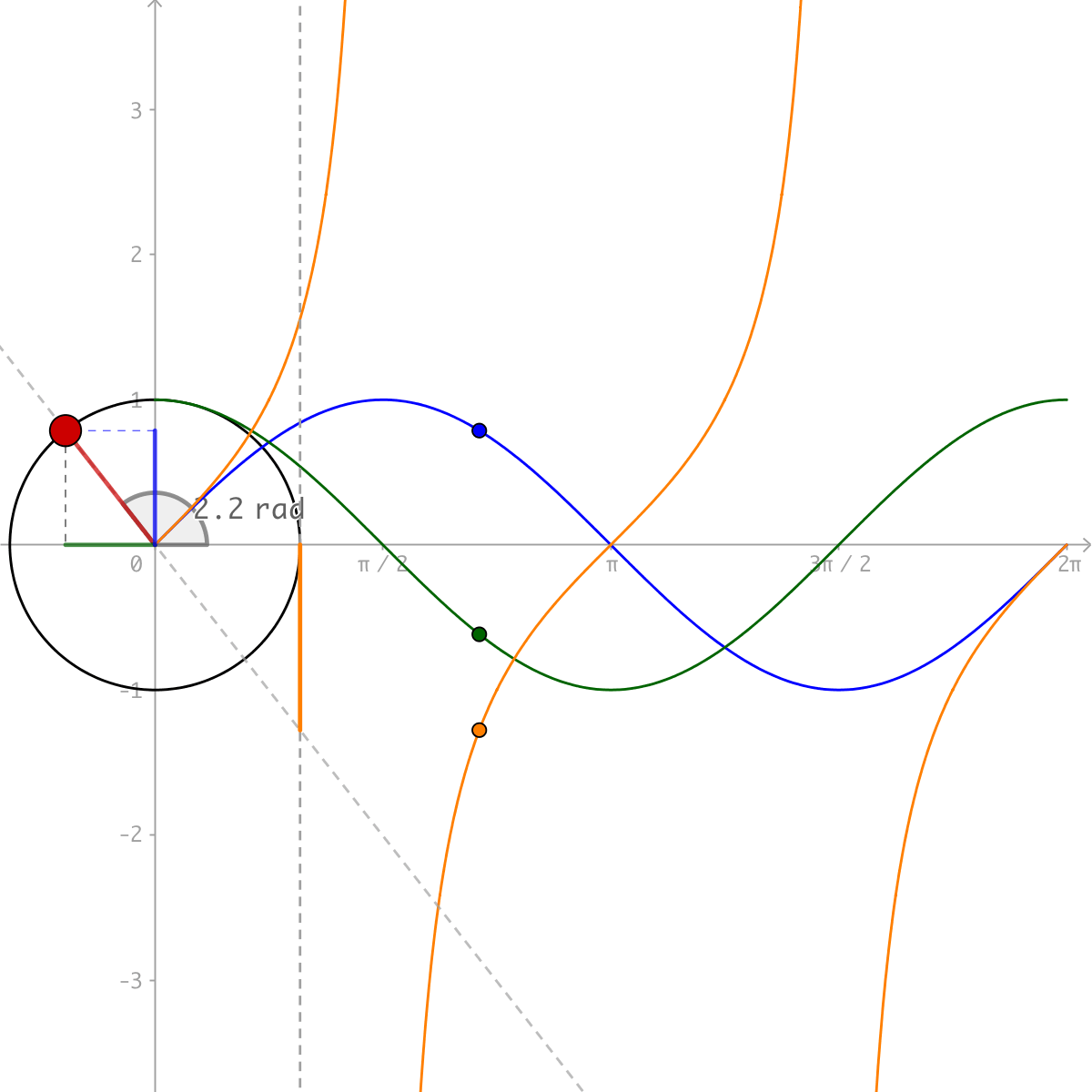
Sine Cosine and Tangent are plotted on the Unit Circle: Source
See it animated here.
You can imagine how using these waves created by the unit circle, could draw fluid trigonometric graphics. Now we're ready to draw a circle!
Take a look at the code by clicking JS on the embedded Pen.
How can we make this circle into a rose? The difference is simply in the equation. Mathematical Roses are drawn using the polar equation:
r = cos(kθ)
So, to transform our circle all we have to do is change the value for var r to a fraction which corresponds with one of the pictured roses, and multiply TWO_PI by the denominator. You'll notice I multiplied the equation by 100. This variable represents the amplitude of the wave, thus influencing the scale of the sketch. We could use any number here to achieve any size rose.

Each formation is determined by a fraction like 2/7 or 3/5,
which will replace k in the above equation.
I've also begun and ended the sketch into a Shape by sandwiching the section where we draw the rose within beginShape(); & endShape(CLOSE);. Since our flower is actually a gestalt of tiny points, this function will close off all the points, creating a solid shape. If you think about it, it's really just a complex spiral.
See what you can sketch with other trig functions.
Finally, a rose for you! Interact with the sliders to change the rose.
Right click and inspect this webpage to see how I have directly embedded the sketch.
